miércoles, 18 de junio de 2014

Inecuaciones Con valor absoluto


INECUACIONES CON VALOR ABSOLUTO 
Propiedades : 
 Para cualquier número real “X” y cualquier número 
positivo “a” : 
1) │ X │ < a a < X < a (también se cumple para ≤). Se puede decir que la desigualdad queda dividida en dos partes : En la primera se “elimina” el módulo de valor 
absoluto y se mantiene lo demás igual (X < a), y en la segunda se “elimina” el módulo 
de valor absoluto, se cambia el sentido de la desigualdad y el signo del miembro de la 
derecha ( X > -a ), la solución viene dada por la INTERSECCIÓN de las dos soluciones 
parciales. 
2) │ X │ > a X > a U X < - a (también se cumple para ≥). Se puede decir que la desigualdad queda dividida en dos partes : En la primera se “elimina” el módulo de valor 
absoluto y se mantiene lo demás igual (X > a), y en la segunda se “elimina” el módulo 
de valor absoluto, se cambia el sentido de la desigualdad y el signo del miembro de la 
derecha ( X < - a ), la solución viene dada por la UNIÓN de las dos soluciones parciales. 
3) │X │ < │a │ X2< a2
 (también se cumple para >, ≥ y ≤). La solución se encuentra aplicando los métodos de resolución de una inecuación cuadrática o de segundo grado. 
4) │ X │ < – a Representa al conjunto vacío (también se cumple para ≤)

Tomado de: http://www.monografias.com/trabajos-pdf4/inecuaciones-valor-absoluto/inecuaciones-valor-absoluto.pdf
Publicadas por a la/s No hay comentarios.:

Inecuaciones Racionales

Recordemos que una expresión racional, es una expresión de la forma:
P ( x ) Q ( x )
Donde P ( x ) y Q ( x ) son polinomios.
Analicemos la gráfica de expresiones racionales. Para ello, vamos a utilizar la aplicación de abajo. Existen 3 segmentos de recta a la derecha de la gráfica rotulados con las letras a,b y c. Los puntos negros a,b y M son movibles y permiten cambiar los valores correspondientes en la expresión:
y = M ( x - a ) ( x - b )
donde a es el intercepto de la gráfica con el eje x (punto A), b es valor donde el denominador es cero y por lo tanto, es el punto donde la expresión no está definida, y M es una constante.

Tomado de: http://quiz.uprm.edu/tutorial_es/Pol_Ineq/pol_ineq_right.xml


Publicadas por a la/s No hay comentarios.:

Inecuaciones Cuadraticas

La inecuación cuadrática o de segundo grado:
x2 − 6x + 8 > 0
La resolveremos aplicando los siguientes pasos:
1ºIgualamos el polinomio del primer miembro a cero y obtenemos las raíces de la ecuación de segundo grado.
x2 − 6x + 8 = 0
solución a la ecuación
2º Representamos estos valores en la recta real. Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo:
gráfica
P(0) = 02 − 6 · 0 + 8 > 0
P(3) = 32 − 6 · 3 + 8 = 17 − 18 < 0
P(5) = 52 − 6 · 5 + 8 = 33 − 30 > 0
3º La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que el polinomio.
gráfica
S = (-∞, 2) Unión (4, ∞)

x2 + 2x +1 ≥ 0
x2 + 2x +1 = 0
solución
(x + 1)2 ≥ 0
Como un número elevado al cuadrado es siempre positivo la solución es R
  Solución
x2 + 2x +1 ≥ 0(x + 1)2 ≥ 0R
x2 + 2x +1 > 0(x + 1)2 > 0R-1
x2 + 2x +1 ≤ 0(x + 1)2 ≤ 0x = − 1
x2 + 2x +1 < 0(x + 1)2 < 0vacio
x2 + x +1 > 0
x2 + x +1 = 0
solución

Cuando no tiene raíces reales, le damos al polinomio cualquier valor si:
El signo obtenido coincide con el de la desigualdad, la solución es R.
El signo obtenido no coincide con el de la desigualdad, no tiene solución.
 Solución
x2 + x +1 ≥ 0R
x2 + x +1 > 0R
x2 + x +1 ≤ 0vacio
x2 + x +1 < 0vacio

Ejercicios de inecuaciones cuadraticas

1 7x2 + 21x − 28 < 0
x2 +3x − 4 < 0
x2 +3x − 4 = 0
solución
P(−6) = (−6)2 +3 · (−6)− 4 > 0
P(0) = 02 +3 · 0 − 4 < 0
P(3) = 32 +3 · 3 − 4 > 0
gráfica
(−4, 1)
2 −x2 + 4x − 7 < 0
x2 − 4x + 7 = 0
solución
P(0) = −02 + 4 ·0 − 7 < 0
S = R
3inecuación
solución
recta
P(−3) = 4 · (−3)2 − 16 > 0
P(0) = 4 · 0 2 − 16 < 0
P(3) = 4 · 3 2 − 16 > 0
gráfica
(-∞ , −2 ] Unión [2, +∞)

44x2 − 4x + 1 ≤ 0
4x2 − 4x + 1 = 0
solución
solución

5inecuación
inecuación
Como el primer factor es siempre positivo, sólo tendremos que estudiar el signo del 2º factor.
ecuación
solución
recta
P(−17) = (−17) 2 + 12 · 17 − 64 > 0
P(0) = 02 + 12 · 0 − 64 < 0
P(5) = 5 2 + 12 · 5 − 64 > 0
gráfica
(-∞, −16] Unión [4, ∞)
6x4 − 25x2 + 144 < 0
x4 − 25x2 + 144 = 0
solución
solución
solución
solución
gráfica
(−4, −3) Unión (−3, 3 ) Unión (3, 4) .
7x4 − 16x2 − 225 ≥ 0 
x4 − 16x2 − 225 = 0 
solución
solución
solución
solución
(x2 - 25) · (x2 + 9) ≥ 0
El segundo factor siempre es positivo y distinto de cero, sólo tenemos que estudiar el signo del 1erfactor.
(x2 − 25) ≥ 0
gráfica
(-∞, −5] Unión [5, +∞)
Tomado En: http://www.vitutor.net/2/9/inecuaciones_cuadraticas.html
Primea Parte


Publicadas por a la/s No hay comentarios.:

Inecuaciones lineales.

Primera Parte
Segunda parte 
Tercera Parte 

Publicadas por a la/s No hay comentarios.:

Inecuaciones lineales.


INTERVALOS E INECUACIONES LINEALES


Existen intervalos abiertos, en los que no se incluyen los extremos; cerrados en los que se incluyen los extremos, y aquellos en que se combinan ambos.
Los intervalos son subconjuntos de los números reales que se pueden representar gráficamente en la recta numérica por un trazo o una semirrecta.
Para representar los intervalos se utiliza una circunferencia vacía en el extremo, si este no se incluye, o rellena si se incluye.

intervalos01
El dibujo superior grafica el intervalo entre todos los números (x) mayores que 7 (x > 7), excluido el 7,  hasta el infinito (+ ∞)

intervalos02
Este dibujo grafica el intervalo entre los números (x) mayores o iguales a 7 (x ≥ 7), incluyendo el 7, hasta el infinito (+ ∞).
Como vemos, la simbología que se utiliza en los casos abiertos (que no incluyen al extremo) son el signo < (menor que)  o  > (mayor que); y para los casos cerrados (que incluyen al extremo) son el signo ≥ (mayor o igual que) o el signo ≤ (menor o igual que).
De acuerdo con la simbología y las características, existen los siguientes tipos de intervalos: 

Intervalo abierto, que se grafica
intervalos03

Se escribe a < x < b (a es menor que equis y equis es menor que b) y también
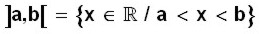
intervalos04(equis pertenece a los reales, tal que a es menor que equis y equis es menor que b)
Esto significa que la solución para la inecuación se encuentra en todos los valores (números reales) entre a y b que hay en la recta numérica, pero que no incluyen ni a  ni b.

Intervalo cerrado, que se grafica
intervalos05
Se escribe a ≤ x ≤ b (a menor o igual que equis, y equis menor a igual que b) y también
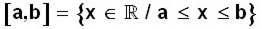
intervalos06(equis pertenece a los reales, tal que a es menor o igual que equis y equis es menor o igual que b).
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y b que hay en la recta numérica, y que incluyen el valor de a  y el de  b.

Intervalo abierto a la izquierda, que se grafica
intervalos07

Se escribe a < x ≤ b (a menor que equis, y equis menor o igual que b) y también
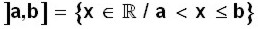
intervalos08  (equis pertenece a los reales, tal que a es menor que equis y equis es menor o igual que b).
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y b que hay en la recta numérica, y que no incluyen el valor de a  pero sí incluyen el valor de  b.

Intervalo abierto a la derecha, que se grafica
intervalos09
Se escribe a ≤ x < b (a menor o igual que equis y equis menor que b) y también
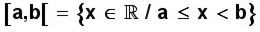
intervalos10 (equis pertenece a  los reales, tal que a es menor o igual que equis y equis es menor que b).
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y b que hay en la recta numérica, y que incluyen el valor de a  pero no incluyen el valor de  b.

Intervalo infinito por la izquierda y abierto, que se grafica
intervalos11
Se escribe x < a (equis es menor que a) y también
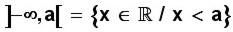
intervalos12(equis pertenece a  los reales, tal que equis es menor que a).
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y el infinito  a la izquierda que hay en la recta numérica, y que no incluyen el valor de a.

Intervalo infinito por la izquierda y cerrado, que se grafica
intervalos13
Se escribe x ≤ a (equis es menor o igual que a) y también
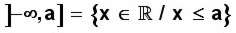
intervalos14 (equis pertenece a  los reales, tal que equis es menor o igual que a).
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y el infinito  a la izquierda que hay en la recta numérica, y que incluyen el valor de a.

Intervalo infinito por la derecha y abierto, que se grafica
intervalos15
Se escribe x > a (equis es mayor que a) y también
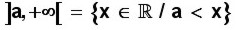
intervalos16 (equis pertenece a los reales, tal que a es menor que equis)
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y el infinito a la derecha que hay en la recta numérica, y que no incluyen el valor de a.

Intervalo infinito por la derecha y cerrado, que se grafica
intervalos17
Se escribe x ≥ a (equis es mayor o igual que a) y también
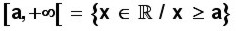
intervalos18 (equis pertenece a los reales, tal que equis es mayor o igual que a)
Esto significa que la solución para la inecuación se encuentra en todos los valores entre a y el infinito a la derecha que hay en la recta numérica, y que incluyen el valor de a.
Como vemos, los intervalos se pueden representar con corchetes, pero también se puede hacer en forma de conjunto:
Ejemplo:
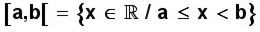
intervalos10 (equis pertenece a  los reales, tal que a es menor o igual que equis y equis es menor que b).
Fuentes Internet:
Ver en youtube:
Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)