Definición de INTERVALOSe llama intervalo al conjunto de números reales comprendidos entre otros dos dados: a y b que se llaman extremos del intervalo.
Intervalo abierto, (a, b), es el conjunto de todos los números reales mayores que a y menores que b.
(a, b) = {x/a
Es decir no incluye los extremos
Intervalo cerrado, [a, b], es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b.
[a, b] = {x / a ≤ x ≤ b}
Incluye los extremos.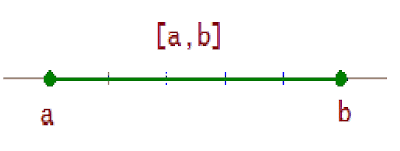
Intervalo semiabierto por la izquierda
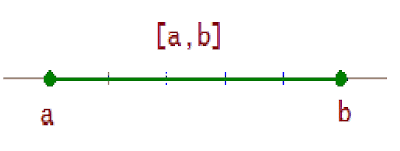Intervalo semiabierto por la izquierda
Intervalo semiabierto por la izquierda, (a, b], es el conjunto de todos los números reales mayores que a y menores o iguales que b.[a, b) = {x / a
Intervalo semiabierto por la derecha, [a, b), es el conjunto de todos los números reales mayores o iguales que a y menores que b.
[a, b) = {x / a ≤ x
En la recta nos queda
Veamos el ejemplo 2
Seguramente notaron que hay un círculo en blanco y otro lleno. ¿Qué explicacin da a esto?, Responda aquí a esta pregunta.
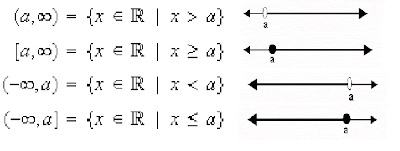
Existen además los intervalos infinitos.
Si a y b son reales, entonces se estableces los siguientes conjuntos infinitos.( en infinito siempre es abierto, es decir su usa parentesis)
INFINITOS ABIERTOS A LA DERECHA, CERRADOS A LA DERECHA, ABIERTOS A LA IZQUIERADA, ABIERTOS A LA DERECHA.
Identificar y definir cada intervalo. segun lo ejemplos anteriores.(dejar el espacio aquí para ello)
En clase veremos ejemplos sobre cada uno de los intervalos.Puede ver ejemplos numericos en http://www.slideshare.net/bethbal/intervalos-numricos
DESIGUALDADES
Se denomina desigualdad a toda expresión que describe la relación entre al menos dos elementos escritos en términos matemáticos, que incluye al menos un símbolo de los siguientes: <; > , ≤,≥. . Por ejemplo 2>1; 6<10.
Una inecuación es una desigualdad donde hay uno o más términos desconocidos llamados incógnitas.
Ejemplos: 2x<2+x; 2x-4>5x; x-5<5-4x
Las inecuaciones pueden ser de primer grado (x con exponente 1 ), y de segundo grado (cuando tiene exponente 2)
En este aparte nos centraremos en la inecuaciones de primer grado o lineales.
OJO: Para las de segundo grado debemos recordar algunos casos de factorización. (En clase me recuerdan para decirles cuales)
RESOLUCION DE UNA INECUACION:
Se procede como en la ecuaciones lineales, recordando que hay dos miembros (izquierdo y derecho) y que podemos pasar términos de un miembro a otro pero se cambia de operación, es decir, que si esta sumando para a restar y viceversa, y si esta multiplicando para a dividir y viceversa.
Algo que debemos tener en cuenta en la inecuaciones es que cuando vayamos a despejar la incógnita y ésta tiene un coeficiente negativo, el signo de la desigualdad cambia, por ejemplo si era < cambia por > y viceversa.
Ejemplos
Hallar la solución de cada inecuación y representarla en notación de conjunto e intervalo.
Las inecuaciones pueden ser de primer grado (x con exponente 1 ), y de segundo grado (cuando tiene exponente 2)
En este aparte nos centraremos en la inecuaciones de primer grado o lineales.
OJO: Para las de segundo grado debemos recordar algunos casos de factorización. (En clase me recuerdan para decirles cuales)
RESOLUCION DE UNA INECUACION:
Se procede como en la ecuaciones lineales, recordando que hay dos miembros (izquierdo y derecho) y que podemos pasar términos de un miembro a otro pero se cambia de operación, es decir, que si esta sumando para a restar y viceversa, y si esta multiplicando para a dividir y viceversa.
Algo que debemos tener en cuenta en la inecuaciones es que cuando vayamos a despejar la incógnita y ésta tiene un coeficiente negativo, el signo de la desigualdad cambia, por ejemplo si era < cambia por > y viceversa.
Ejemplos
Hallar la solución de cada inecuación y representarla en notación de conjunto e intervalo.
En la recta nos queda
Veamos el ejemplo 2
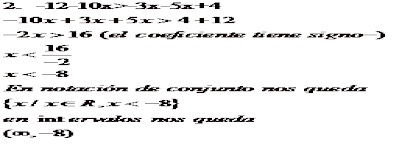
ejemplo 3.
La grafica es.
Ejemplo 4.
En la recta nos queda
No hay comentarios.:
Publicar un comentario